高等数学

微积分

微积分阐述的是一种微分和积分的思想，从几何上来讲，主要是求曲线函数在某时刻的增量(微分)…

极限

这里将函数的极限，函数的极限存在意义是在某个点上，该函数的左右极限都存在，这样才称该函数存在极限。在该点上函数不一定需要有定义. 比如说 $$f(x) = \frac{1}{x} $$. 当 $$ x \to 0$$ 时,极限为无穷大。虽然该函数在 $$f(0)$$ 处没定义。

连续

函数连续的意义是该函数在该点的左右都连续，且在该点有定义。一个函数连续一定表示该函数有极限，但有极限并不一定表示该函数是连续的。

导数

导数代表的是该函数在某一时刻的变化率大小.从极限的定义上来讲就是当变化率趋近于0时，函数值的变化/变化率 的极限。

微分

微分描述的是一种变化量，除了这一点外，和导数没啥区别，它的定义就是 $$d_y = f’(x) * d_x$$

matlab上计算极限用的时limit命令，导数用的时diff命令。声明变量用的是 syms 命令.

罗尔定理

成立条件:

1. $$f(x)$$ 在区间 [a,b] 上是连续的
2. $$f(x)$$在区间(a,b)上是可导的
3. $$f(a) = f(b)$$

结论: 在$$(a,b)$$上存在一点$$\epsilon$$，使得 $$f’(\epsilon) = 0$$

拉格朗日微分中值定理

成立条件:

1. $$f(x)$$在区间 [a,b] 上是连续的
2. $$f(x)$$在区间(a,b)上是可导的

结论: 在$$(a,b)$$上存在一点$$\epsilon$$，使得 $$ f(b)-f(a) = f’(\epsilon)(b-a)$$ 成立

柯西定理

成立条件:

设函数 $$f(x),g(x)$$,满足:

1. 在闭区间$$[a,b]$$上连续
2. 在开区间$$(a,b)$$上可导
3. 对任意 $$x (a,b), g(x) \ne 0$$

结论: 在开区间$$(a,b)$$上存在一点$$\epsilon$$ 使得$$\frac{f(b)-f(a)}{g(b)-g(a)} = \frac{f’(\epsilon)}{g’(\epsilon)}$$成立

泰勒定理

泰勒定理主要是用来对在区间求具体变量 $(x_0)$ 的函数值时将其等价于求在该区间内 $(x-x_0)$ 的 $n$ 项多项式之和 $P_n(x)$。

$f(x)$ $ \approx $ $a_0 + a_1(x-x_0) + a_2(x-x_0)^2 + a_3(x-x_0)^3+ … + a_n(x-x_0)^n$

这个就可以近似的表示 $f(x)$ , 要求 $|f(x) - P_n(x)| = o\lfloor x-x_0 \rfloor ^n$ (关于 $x_0$ 的一个高阶无穷小), 接下来我们来求变量 $a_0,a_1,a_2, … , a_n$ 的表达式.

假设 $f(x) = P_n(x) $ 的倒数随着 $n$ 的增加一直存成立。

因为 $$P_n(x) = a_0 + a_1(x-x_0) + a_2(x-x_0)^2 + a_3(x-x_0)^3+ … + a_n(x-x_0)^n$$ , 有

$$ P_n’(x) = a_1 + 2 a_2(x-x_0) + 3 a_3 (x-x_0)^2 + … + n a_n * (x-x_0)^{(n-1)}$$

$$ P_n’’(x)= 2a_2 + 32a_3(x-x_0) + … + n(n-1)a_n(x-x_0)^{(n-2)}$$

$$ P_n^{(n)}(x) = n!*a_n$$

可得:

$$a_0 = f(x_0)$$

$$a_1 = P_1’(x) = f’(x_0)$$

$$a_2 = \frac{1}{2} * f’’(x_0)$$

$$a_n = \frac{1}{n!} * f^n(x_0)$$

代入原式可得:

$$P_n(x) = f(x_0) + f’(x_0)(x-x_0) + \frac{1}{2!}f’’(x_0)(x-x_0)^2 + … +\frac{1}{n!} f^n(x_0)*(x-x_0)^n \approx f(x)$$

只要能够证明它的余项式为 $\lfloor x-x_0 \rfloor$ 的高阶无穷小量，那么我们就可以证明 $f(x)$ 和 $P_n(x)$ 近似相等。

以上就是我们的 泰勒中值定理 的推论过程, 它的具体定义是:

函数 $f(x)$ 在开区间 $(a,b)$ 具有 $(n+1)$ 阶导数，则当 $x \in (a,b)$ 时，$f(x)$ 可以表示为一个 $(x-x_0)$ 的一个$n$ 次多项式与余项 $R_n(x)$ 的和。公式表示如下

$$f(x) = f(x_0) + f’(x_0)(x-x_0) + \frac{1}{2!}f’’(x_0)(x-x_0)^2 + … +\frac{1}{n!} f^n(x_0)*(x-x_0)^n + R_n(x)$$

其中 $R_n(x)$ 的值一般为拉格朗日型余项。值为:

$$R_n(x) = f(x) - P_n(x) = \frac{1}{(n+1)!}f^{(n+1)}(\xi)(x-x_0)^{(n+1)}$$

所以可得 泰勒公式

$$f(x) = f(x_0) + f’(x_0)(x-x_0) + \frac{1}{2!}f’’(x_0)(x-x_0)^2 + … +\frac{1}{n!} f^n(x_0)*(x-x_0)^n +\frac{1}{(n+1)!}f^{(n+1)}(\xi)(x-x_0)^{(n+1)}$$

matlab实践:

求函数在$[-4，2]$极值: $ x^3 + 2x^2 - 5x +1$

首先求该函数的一阶导数:

>> syms x
>> y =  x^3 + 2*x^2 - 5*x +1 
>> dy = diff(y)
 
    3*x^2 + 4*x - 5

再求驻点

>> xz = solve(dy)
>> xz = double(xz)
xz =

   -2.1196
    0.7863

得到两个驻点 $-2.1196$ 和 $0.7863$

再求二阶导数,判断该驻点对应的值是极大值还是极小值

>> ddy = diff(dy)
	
	6*x + 4

代入两驻点得

>> x1 = limit(ddy,x,-2.1196)
x1 =
 
  -10897/1250
>> x2 = limit(ddy,x,0.7863)
x2 =
 
   43589/5000

可知当$x$趋向于两驻点时，它的二阶导数的值一个为正数，一个为负数。可知在 $x_1$ 点，函数存在极大值点。在 $x_2$ 点，函数存在极小值点。也可以通过画图明显看出结果

>> fplot('x^3 + 2*x^2 - 5*x + 1',[-4,2])

注意这里的 $fplot$ 函数第一个参数只接受常量表达式.

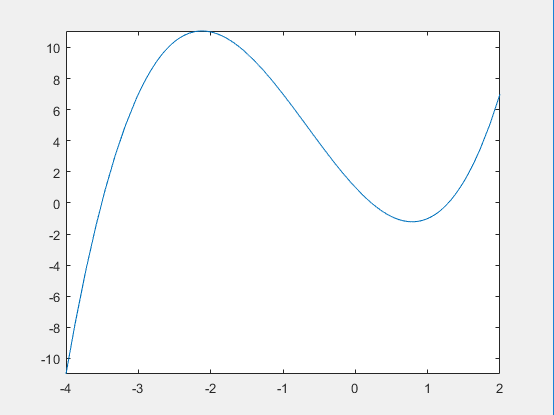
也可以用 $fminbnd$ 函数来直接求在区间上的最小值。

>>  fminbnd('x^3 + 2*x^2 -5*x + 1',-4,2)
ans =

    0.7863

求最大值只需给函数加个负号即可

积分

不定积分

要了解积分的概念先了解一下原函数的概念:

$f(x)$的定义域属于 $I$ ，设 存在 函数 $F(x)$ 也在区间 $I$ 上有意义并且可导。 当 $F’(x) = f(x) $ $x \in I$ 或者 $dF(x) = f(x) dx $ $x \in I$ 成立时，则称 $F(x)$ 为 $f(x)$ 的原函数。

设 $C$ 为常数，$\because (F(x) + C)’ = F’(x) = f(x) \therefore F(x) + c $ 也是$f(x)$ 的原函数。

原函数的主要性质:

1. 无穷性。
2. 相关性(原函数之间的差的导数为一个常数)。
3. 在某个区间内连续的函数必有原函数，因为初等函数在定义域内时连续的，所以初等函数的原函数有无穷多个。

定义:

函数 $f(x)$ 在某区间的所有原函数的集合称为 $f(x)$ 的不定积分,记作: $\lmoustache f(x)d_x$

不定积分的主要性质:

• 不定积分的导数等于原函数. $(\lmoustache f(x)d_x)’ = f(x)$
• 不定积分的微分等于被积表达式. $\lmoustache f’(x) d_x = f(x) + C $ 或者 $\lmoustache df(x) = f(x) + C$

不定积分的表达式: $\lmoustache f(x)dx = F(x) + C$

定积分

定义:

函数 $f(x)$ 在区间 $[a,b]$ 上是有界函数，在其上取 $n-1$ 个分点，使得 $a = x_0 < x_1 < x_2 < …. < x_n = b$，把区间 $[a,b]$ 划分成 $n$ 个小区间 $[x_0,x_1],[x_1,x_2],[x_3,x4],[x{i -1},xi],[x{n-1},x_n]$, 各个小区间的长度为$\vartriangle x = xi - x {i-1}$ $ x=(1,2,…,n)$, 在每个小区间 $[x_{i-1},x_i]$ 上任取一点 $\xii$ , 作和式 $\sum{i=1}^{n}f(\xi_i)\vartriangle x_i$, 记 $\vartriangle x = max{\vartriangle x_1,\vartriangle x_2, \vartriangle x_3 … \vartriangle x_n}$ 。无论区间 $[a,b]$ 怎样划分，也不管 $\xii$ 怎样的取获取，当 $\vartriangle x \to 0 $ 时，极限 $lim {\vartriangle x \to 0} \sum_{i=1}^n f(\xi_i)\vartriangle x_i$ 存在且为值 $I$ , 则称 $I$ 为函数 $f(x)$ 在区间 $[a,b]$ 上的定积分,简称为积分，记作: $\lmoustache _a^b f(x) dx$

定积分的函数表达式:

$\lmoustache a ^b f(x)dx = lim {\vartriangle x \to 0} \sum_{i=1}^n f(\xi_i)\vartriangle x_i = F(b) - F(a)$

这也就是 牛顿-布莱尼茨公式 .

matlab实践

matlab种对积分求不定积分表达式和定积分对的积分值用的都是int方法，下面来看一下对 $y = sin(x)$ 的不定积分和在 $(0,\frac{\pi}{2})$ 的积分值怎么求:

>> syms x
>> y = sin(x)
 
y =
 
sin(x)
 
>> int(y)
 
ans =
 
-cos(x)
>> int(y,x,0,pi/2)
 
ans =
 
1

求解微分方程:

matlab 中用 $dsolve$ 方法来求解微分方程的通解和特解。其中表示y的 $k$ 阶导数用 $Dky$ 来表示。例如:

求 ，$(1+x^2)y’’ = 2x*y’$ 当 $y(0) = 1$ $y’(0) = 3$ 的特解:

>> syms x
>> eqn='(1+x^2)*D2y = 2*x*Dy'

eqn =

    '(1+x^2)*D2y = 2*x*Dy'

>> dsolve(eqn,'y(0)=1,Dy(0)=3','x')
 
ans =
 
x*(x^2 + 3) + 1

$dsolve$ 方法的第二个参数为方程的初始条件，若是求通解，就不需要加上这个参数了。$x$ 是表示对 $x$ 求微分。默认是对 $t$ 求微分

好想法(习题解析)

$question1: $ 有隐式函数 $( w(x) + 1 )* exp(w(x)) = x$ , 当 $x = 1$ 时，$w(x) = 0$ .求 $w(3/2)$ 的近似值.

$answer:$ 这个题目需要用到线性逼近的思路来做，因为所求的点为 3/2，可以近似的认为 $w(\frac{3}{2})$ 和 $w(1)$ 的值在一条直线上。所以根据 $n=1$ 项的泰勒展开式可得在 $x=1$ 时，该线性函数方程式为 $w(x) \approx w(1) + w’(1)(x-1) $ .现在只需求得 $w’(1)$ 的值即可。这个对两边求导化简即可。

Read More